[자료구조/알고리즘] 트리, 이진 탐색 트리, 이진 힙
> 트리(tree)
나무를 뒤집은 모습으로 계층 구조를 표현하기에 적합한 자료구조다. 연결 리스트와 같이 메모리 칸을 이용해 정보를 저장하며, 각 메모리 칸은 다른 칸의 위치를 가르키는 포인터를 가진다. 다만 그 모양이 일방향 혹은 양방향의 사슬이 아닌, 하나의 뿌리를 둔 나무의 모양을 띈다는 점에서 다르다.
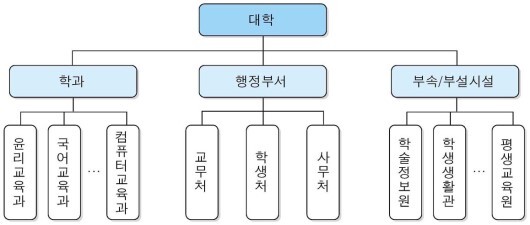
각 칸을 노드(node), 포인터를 엣지(edge), 그리고 트리의 최상위 정점은 뿌리(root)라 부르며, 노드간 상하관계를 부모자식관계로 표현한다. (학과의 자식 노드는 윤리교육과, 국어교육과, ... 컴퓨터교육과의 부모노드는 학과)
자식 노드를 하나도 갖지 않는 노드들은 잎(leaf)이라 부른다. 한 노드에서 뿌리까지의 경로의 길이를 깊이(level), 트리에서 가장 깊은 노드의 깊이가 트리의 높이(height)에 해당한다.
> 이진 탐색 트리(binary search tree)
이진 트리(binary tree) = 각각의 노드가 최대 두 개의 자식 노드를 가지는 트리
이진 탐색 트리(binary search tree) = 이진 트리 중에서도 아래의 조건을 만족하는 것. 데이터의 삽입, 삭제, 탐색 등이 자주 발생하는 경우에 효율적인 구조다.
- 같은 값을 갖는 노드가 없다.
- 왼쪽 서브 트리에 있는 모든 데이터는 현재 노드의 값보다 작고, 오른쪽 서브 트리에 있는 모든 노드의 데이터는 현재 노드의 값보다 크다.

위의 예에서 1, 2로 표기한 부분은 전체 이진 트리의 일부이면서, 트리의 성격을 만족하므로 노드 7을 기준으로 각각 왼쪽 서브 트리와 오른쪽 서브 트리라 할 수 있다. 이때 1의 노드들은 모두 7보다 작고, 2의 노드들은 모두 7보다 크므로 두 번째 조건을 만족한다. 모든 노드들에 대해 해당 조건이 만족함을 확인할 수 있다.
> 트리 균형 잡기, 자가 균형 이진 탐색 트리
이진 탐색 트리의 조건을 만족하면서 노드들을 추가하다보면, 트리가 한 쪽으로만 깊어지면서 불균형이 생기는 경우가 있다. 예시는 아래와 같다.

이는 원래의 트리의 구조를 유지한 채로 노드들을 아래에 붙이기 때문에 발생하는데, 데이터 접근성에 비효율을 초래한다. 본래의 이진 트리는 균형 잡기(balancing)가 필요한 상황이지만, 노드를 추가/삭제하는 과정에서 트리의 균형을 유지하는 트리가 바로 자가 균형 이진 탐색 트리다. 정렬된 리스트, 연관 배열(associative array), 우선 순위 큐, 집합 등의 구현에 쓰인다.

1) 레드-블랙 트리
자가 균형 이진 탐색 트리의 대표적 예시. 연관 배열과 사전(맵) 등의 구현에 쓰인다고 한다. 이진 탐색 트리이면서 아래의 조건을 추가로 만족해야 한다. O(log n)의 시간복잡도로 삽입, 삭제, 검색을 할 수 있다는 장점이 있다.
- 노드는 레드 혹은 블랙 중의 하나이다.
- 루트 노드는 블랙이다.
- 모든 리프 노드들(NIL)은 블랙이다.
- 레드 노드의 자식노드 양쪽은 언제나 모두 블랙이다. (즉, 레드 노드는 연달아 나타날 수 없으며, 블랙 노드만이 레드 노드의 부모 노드가 될 수 있다)
- 어떤 노드로부터 시작되어 그에 속한 하위 리프 노드에 도달하는 모든 경로에는 리프 노드를 제외하면 모두 같은 개수의 블랙 노드가 있다.

2) AVL 트리(Adelson-Velsky and Landis)
자가 균형 이진 탐색 트리의 하나. 두 자식 서브트리의 높이는 항상 최대 1만큼 차이나도록 유지하는 트리. 어떤 시점에서 높이 차이가 1보다 커지면 스스로 균형을 잡는다. 검색, 삽입, 삭제는 모두 평균과 최악의 경우 O(log n)의 시간복잡도가 걸린다. 레드-블랙 트리와 비교하면 항목을 추가, 제거하는 데 시간이 조금 더 걸리며, 균형을 잡는데 있어서는 더 뛰어나다. 항목의 조회 속도가 빠른 편이어서 읽기 작업이 빈번한 상황에 최적화를 위해 쓰인다.
3) 이진 힙(binary heap)
이진 탐색 트리 중 최대, 최소에 빠르게 접근하는 데에 특화된 트리. https://mingchin.tistory.com/113 참고