[자료구조/알고리즘] 그래프, DFS, BFS
1) 그래프
데이터의 다양한 표현 방법 중 하나로, 꼭짓점(vertex) 혹은 노드(node)와 변(edge)으로 구성된 한정된 자료구조를 말한다. 데이터 간의 연결성을 표현하는 데에 그 장점이 있는 자료구조로, 지도나 도로 등의 경로에서의 최단거리 문제 등에서 활용된다. 코딩 테스트에서 그래프 탐색 문제는 자주 출제되는 유형이기도 하다.
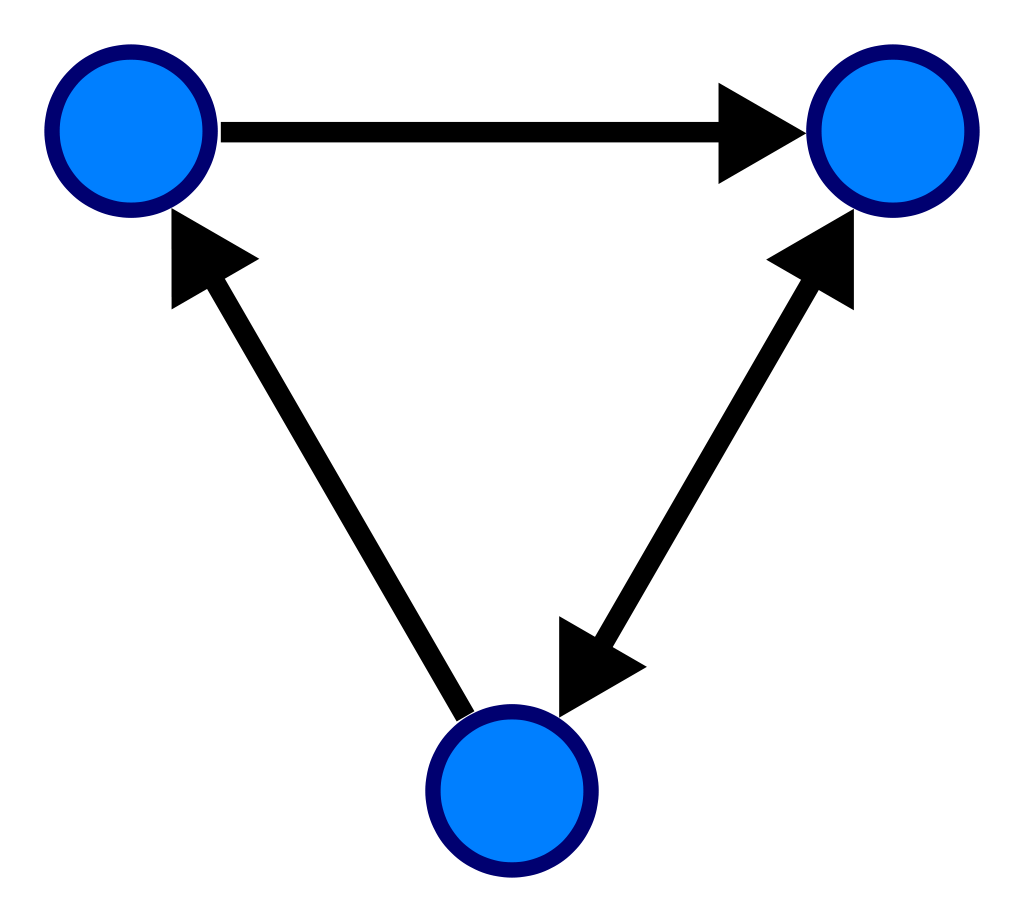
경우에 따라 노드 간의 연결(간선_edge)에 방향성이 있기도, 없기도 하다. 즉 단방향 연결과 양방향 연결이 모두 가능하다. 간선에 가중치가 존재하기도 하며(ex_ 도로의 통행료, 도로 선택시 걸리는 시간 등), 순환이 가능한지 여부나 모든 노드가 연결되어있는지 여부에 따라 그 종류를 구분하기도 한다(사이클 vs 비순환 그래프, 완전 그래프).
구현은 아래의 두 가지 방법으로 가능하다.
① 인접 리스트
배열, 사전 등을 활용해 각 노드들이 연결되어 있는 노드들을 나열함으로써 그래프를 표현할 수 있다. 아래의 예시는 각 노드들이 모두 다른 노드들과 (연결되어 있다면) 양방향으로 연결된 그래프 표현의 예시다.
# 그래프의 표현 예시 (1)
0: 1, 2
1: 0, 2
2: 0, 1, 3
3: 2
4: 5, 6
5: 4, 6
6: 4, 5이는 무방향 그래프라고도 하며, 당연히도 edge의 갯수는 짝수이어야한다.
한 노드에 연결된 다른 노드를 한 번에 파악할 수 있다는 장점이 있다.
② 인접 행렬
각 인덱스에 해당하는 노드들의 다른 노드와의 연결 여부를 Boolean 행렬로 표현하는 방법이다.
# 그래프의 표현 예시 (2)
if(두 노드 (i, j)사이의 edge가 존재하는 경우):
matrix[i][j] = 1;
else:
matrix[i][j] = 0;
[[0, 1, 1, 0, 0, 0, 0],
[1, 0, 1, 0, 0, 0, 0],
[1, 1, 0, 1, 0, 0, 0],
[0, 0, 1, 0, 0, 0, 0],
[0, 0, 0, 0, 0, 1, 1],
[0, 0, 0, 0, 1, 0, 1],
[0, 0, 0, 0, 1, 1, 0]]위 ①의 예시와 같은 예를 표현한 것이다. 무방향 그래프라면 대칭 행렬(Symmetric Matrix)이어야한다.
연결되지 않은 모든 노드들에 대해 0으로 표현해주기 때문에 같은 그래프를 표현해도 인접 리스트를 이용할 때보다 데이터 양이 많다(edge가 많을 수록 비슷해짐).
한 노드에 연결된 다른 노드를 파악하려면 다른 모든 노드에 대해 탐색해야한다는 단점이 있다. 반대로 두 노드 사이의 연결 여부는 O(1)의 시간 복잡도로 파악할 수 있다.
그래프의 노드들을 순회하며 원하는 정보를 얻는 것을 그래프 탐색이라 하는데, 보통 아래의 두 가지를 말한다.
2) DFS(Depth-First Search)
말 그대로 '깊이 우선 탐색'이다. 하나의 노드에서 시작해 더이상 인접한 노드가 없을 때까지 깊이 들어가 탐색하는 것을 우선으로 하는 방법이다. 스택(stack) 혹은 재귀 함수를 이용해 구현할 수 있는데, 그 방법은 아래와 같다.
① 탐색 시작 노드를 스택에 삽입하고 방문 처리를 한다.
②-1 스택의 최상단 노드에 방문하지 않은 인접한 노드가 있는 경우, 그 노드를 스택에 넣고 방문 처리한다.
②-2 스택의 최상단 노드에 대해 방문하지 않은 인접한 노드가 없으면 스택에서 최상단 노드를 꺼낸다.
③ 모든 노드를 방문할 때까지 ②를 반복한다.
위 예로 든 그래프로 재귀함수를 이용해 dfs를 구현하면 다음과 같다.
# 위 예시의 그래프
g = [[1,2],[0,2],[0,1,3],[2],[5,6],[4,6],[4,5]]
# dfs의 구현
visit = [False]*len(g)
def dfs(graph, start, visit):
visit[start] = True
print(start, end = ' ')
for i in graph[start]:
if not visit[i]:
dfs(graph, i, visit)
dfs(g, 1, visit)
dfs(g, 5, visit)
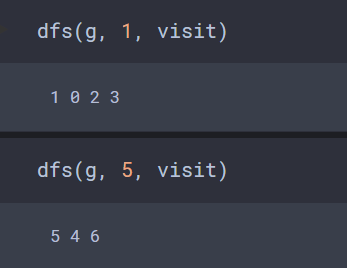
(0,1,2,3)의 노드들과 (4,5,6)의 노드들 사이의 연결이 없기 때문에 위와 같은 결과가 나온다.
3) BFS(Breadth-First Search)
'너비 우선 탐색'이다. 하나의 노드를 기준으로 가까운 노드부터 우선적으로 탐색하는 방법이다. 큐(queue)를 이용해 구현할 수 있다.
① 탐색 시작 노드를 큐에 삽입하고 방문 처리를 한다.
② 큐에서 노드를 꺼내어 인접한 노드 중 방문하지 않은 모든 노드를 큐에 넣고 방문 처리한다.
③ 모든 노드를 방문할 때까지 ②를 반복한다.
다시 같은 예로 bfs를 구현하면 아래와 같다.
from collections import deque
g = [[1,2],[0,2],[0,1,3],[2],[5,6],[4,6],[4,5]]
visit = [False]*len(g)
def bfs(graph, start, visit):
q= deque([start])
visit[start] = True
while q:
now = q.popleft()
print(now, end=' ')
for i in graph[now]:
if not visit[i]:
q.append(i)
visit[i] = True
bfs(g, 3, visit)
bfs(g, 6, visit)
마찬가지로 (0,1,2,3)의 노드들과 (4,5,6)의 노드들 사이의 연결이 없기 때문에 위와 같은 결과가 나온다.