기록하는삶
[인공지능 수학/AI Math] 엔트로피와 크로스엔트로피, KL Divergence, JS Divergence 본문
[인공지능 수학/AI Math] 엔트로피와 크로스엔트로피, KL Divergence, JS Divergence
mingchin 2022. 3. 11. 14:47
엔트로피라는 개념은 열역학적 정의와 통계학적 정의 두 가지가 있는데, 이중 인공지능 분야에서 주로 다뤄지는 것은 통계학적 정의다. 엔트로피의 통계학적 정의는 정보 이론에 그 바탕을 두고 있는데, 정보를 표현하는 단위에 따라 또 다시 여러가지 표현이 가능하다. 이 글에서는 모든 정보를 0과 1로 이진화해 표현하는 경우에 해당하는 섀년의 아이디어를 중심으로 정리해본다.
1) 엔트로피(Entropy)
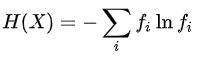
정의가 다소 난해하다. 엔트로피의 정의는 어떤 정보를 표현하는데 필요한 최소 자원량의 기댓값이다. 또는 정보 자체의 기댓값이라 표현할 수도 있다. 여기서의 '정보'란 그것이 나타날 확률에 반비례하는 값으로 정보가 등장할 확률에 대한 음의 로그로 표현하게 되는데, 이는 더 자주 일어나는 일은 정보가 적고 자주 일어나지 않는 일은 정보가 많다고 생각하는 것과 같다. 예를 들어 매일 카페에 가서 커피를 주문하는 내가 10번 중 9번은 아이스아메리카노만 주문한다면(p=0.9) 이는 당연한 일이어서 판매자에게 새로운 정보가 아니다. 내가 더 적은 빈도로 주문하는 아이스바닐라라떼(p=0.1)가 있다면 이는 상대적으로 더 새로운, 큰 정보량이라고 생각하는 것이다.
이러한 방식으로 나의 커피 주문을 표현해야, 즉 상대적으로 자주 표현해야하는 아아의 주문은 적은 정보량으로 더 적은 빈도로 표현하는 아바라의 주문은 더 큰 정보량으로 표현할 때 최소의 자원(적은 비트를 사용해)으로 동일한 정보를 표현할 수 있게 된다. i개의 이산공간에 대한 엔트로피의 값은 그 확률분포가 uniform할 때 최대라고 한다.
위의 예시의 0.9의 확률로 아이스아메리카노를 주문하는 상황에 대한 엔트로피보다, 내가 반반의 확률로 아아와 아바라를 주문하는 상황에 대한 엔트로피가 더 높다. "엔트로피가 높다 = 정보가 많다 = (정보가 많아 어느 것을 골라야할 지) 다음 예측이 불확실하다" 정도로 받아들여도 좋을 것 같다. (반반으로 주문할 때가 9:1로 주문할 때보다 다음으로 무엇을 주문할 지 예측하기가 불확실하다.)
2) Cross-Entropy
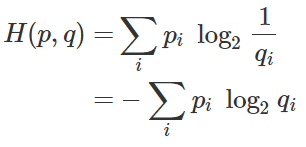
엔트로피 수식에서, 정보량을 표현할 때 실제 확률(p_i)가 아닌 예측 확률(q_i)ㅇ르 사용했을 때의 기댓값이다. 실제의 확률 분포가 예측 확률 분포와 동일할 때 엔트로피와 동일한 값을 갖기 때문에, H(p,q) >= H(p)를 항상 만족한다. 따라서 예측 분포가 실제 분포와 유사할수록 크로스엔트로피는 작아지고, 실제 분포와 다를수록 크로스엔트로피 값은 커진다. 기계학습의 분류문제는 원래 이산공간의 확률분포를 학습하는 것이 목표이므로, 이 크로스엔트로피를 최소화하는 방향으로 학습을 진행하게 된다.(loss를 cross-entopy로 설정)
3) KL Divergence(Kullback–Leibler Divergence)
두 확률 분포 간의 차이를 수치화하는 함수로, 어떤 확률 분포에 대해 그 분포를 근사하는 다른 분포를 사용해 샘플링을 한다면 발생할 수 있는 정보 엔트로피의 차이를 구한다. 말이 거창하지 별 게 아니라, 위에서 구한 크로스엔트로피와 엔트로피의 차가 바로 KL Divergence다. 두 확률 분포가 유사할수록 0에 가까우며, 그렇지 않을수록 그 값이 커진다.
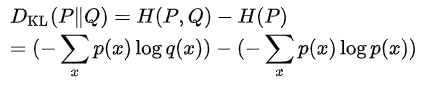
위에서 살펴본 것에 따르면 KLD 값은 항상 0보다 크거나 같으며, symmetric 하지 않다. (DKL(P||Q) != DKL(Q||P)) symmetric 하지 않기 때문에 두 확률 분포의 유사도 측정에 활용될 수는 있으나, 거리라고 표현하기는 어렵다.
4) Jensen–Shannon Divergence

KLD가 symmetric 하지 않음을 보완하기 위한 측정법이다. 두 확률 분포와 두 확률 분포의 평균과의 KLD의 평균값이다. 이 값은 symmetric 하여 거리로 활용될 수 있으며, 두 분포가 유사할수록 0에 가깝다.
[참고자료]
'AI > 인공지능 수학' 카테고리의 다른 글
| [인공지능 수학] 조건부 확률 용어 정리, Precision, Recall, F1-score (0) | 2022.03.01 |
|---|

