기록하는삶
[논문 리뷰] Neural Collaborative Filtering(2017) 본문
1. ABSTRACT & INTRODUCTION
CV, NLP, 음성 인식 등의 분야에 비해 DNN의 활용에 대한 연구가 상대적으로 덜 이루어진 추천 시스템 영역에서의 DNN적용 방안을 제시한 논문이다. 기존에는 딥러닝이 활용되더라도 보조적인 수단으로 사용되고 MF(Matrix Factorization) 방식이 중심이 되는 것이 일반적이었다. 본 논문은 이전 CF(Collaborative Filtering) 방법론들이 implicit feedback을 데이터로 사용하기 어려웠던 단점을 극복할 수 있는 DNN 기반의 NCF(Neural network-based Collaborative Filtering)를 제안한다. 본 논문이 주장하는 novelty는 아래의 세 가지다.
1. We present a neural network architecture to model latent features of users and items and devise a general framework NCF for collaborative filtering based on neural networks.
-> NN 기반의 collaborative filtering 설계
2. We show that MF can be interpreted as a specialization of NCF and utilize a multi-layer perceptron to endow
NCF modelling with a high level of non-linearities.
-> MF의 일반화된 모형이 NCF임을 보이고, MLP를 사용해 더 복잡한 non-linearity를 모델링
3. We perform extensive experiments on two real-world datasets to demonstrate the effectiveness of our NCF
approaches and the promise of deep learning for collaborative filtering.
-> 두 개의 데이터셋(MovieLens, Pinterest)을 사용한 실험으로 NCF의 효과성을 입증
2. PRELIMINARIES (기존 연구의 방향성)
2.1 Implicit Data의 활용

기존의 방법론들은 implicit data를 활용하기 위해 유저와 아이템간 상호작용 여부를 (1)과 같이 이진화해 표현했다. 이때 상호작용이 존재하지 않아 0으로 표기된 아이템의 경우 유저가 해당 아이템을 좋아하지 않았거나, 아직까지 발견하지 못했을 수 있다. (다만 알 길이 없다.) 따라서 이를 모델 파라미터 학습에 활용할 때, 하나의 목표치(평점, 선호도 등)를 예측하는 pointwise loss를 목적 함수로 설정하는 경우에는 0으로 표기된 모든 아이템을 negative feedback으로 간주하거나, 그 중 일부를 sample해 negative feedback으로 활용했다. 두 아이템 간 ranking을 예측하는 pairwise loss를 목적 함수로 설정하는 경우에는 1로 표기된 아이템들이 0으로 표기된 아이템들보다 좋은 ranking을 받고, 또 그 차이가 maximize 되는 방향으로 학습을 진행하게 하였다.
→ NCF는 loss function으로 pointwise loss와 pairwise loss를 모두 사용할 수 있다.
2.2 Matrix Factorization
유저와 아이템에 대한 latent matrix를 생성하고, 이들의 inner product 만으로 둘 사이의 관계성을 학습하는 기존의 MF 방식은 보다 복잡한 관계성을 표현하는 데에 한계가 있다.

위 예시는 item의 수가 5이고 latent space의 차원이 2인(k=2) MF를 모델링하고자 할 때 발생할 수 있는 모순을 보여준다. 원래 item vector들이 가지는 차원보다 작은 차원으로 축소하기 때문에, 표현력의 한계가 존재하고 이로 인해 위와 같은 상황이 생길 가능성이 높다. 이를 해결하는 간단한 방법은 latent space의 차원(k)을 늘리는 것인데, 이는 연산량을 증가시키고 과적합의 위험을 높일 수 있다. (특히나 user-item matrix가 대부분 sparse하기 때문에 더더욱 그렇다.)
3. NEURAL COLLABORATIVE FILTERING(NCF)

모델은 위처럼 GMF와 MLP 두 축으로 구성된다.
3.1 General Framework
input으로 사용되는 유저와 아이템의 feature vector의 경우 context-aware, content-based, neighbor-based 등의 방법론들을 범용적으로 적용하여 만들 수 있으나, 해당 논문에서는 유저와 아이템의 identity 정보만을 활용했다. 우측의 MLP layer 1은 embedding layer에 해당하며, pointwise loss를 사용해 y_hat을 예측하돌고 했으나, BPR(Bayesian Personalized Ranking) 혹은 margin-based loss 등을 사용한 pairwise learning도 가능하다고 저자는 주장하고 있다.

squared loss를 정의하면 위와 같은데, 본래 target값인 y가 0: 관심 없음(interaction x) 혹은 1: 관심 있음(interaction o)둘 중 하나를 가진다는 것을 고려하면, y가 Gaussian distribution을 가질리 없으므로 적합하지 않다고 판단했다. (squared loss는 target의 분포가 Gaussian distribution임을 가정하는 듯 하다 - Probabilistic matrix factorization_2008 참고)
이에 예측 값에 확률적 설명을 부여하기 위해 the Logistic or Probit function 등을 마지막 activation function으로 사용해, [0,1]의 값을 예측하도록 했다.(즉 예측 값인 y_hat은 유저 u가 아이템 i에 interaction을 발생시킬 확률을 의미하게 된다.) 이에 따라 likelihood function을 정의하고 negative logarithm을 취하면 아래와 같은데 이는 결국 BCE의 수식과 같아진다. 무슨 BCE 썼단 소리를 이렇게 어렵게 해

3.2 Generalized Matrix Factorization (GMF)

a_out은 activation function을, h는 edge weights를 의미한다. a_out = identity function & h = uniform vector of 1이면 기존의 MF를 표현할 수 있는 형태여서, 해당 논문이 MF의 일반화된 표현이라는 뜻의 GMF라는 명명을 하였다. 이 논문에서는 a_out을 sigmoid로, h는 BCE(Binary Cross Entropy _ aka. log loss)를 통해 데이터로부터 학습하도록 했다.
3.3 Multi-Layer Perceptron (MLP)
mlp는 특이점이 없다. sigmoid, hyperbolic tangent (tanh), and ReLU 등등 써봤는데 ReLU가 역시 최고란다. 그리고 위로 갈수록 좁아지는 tower pattern을 사용했다.
3.4 그 외의 특이점

GMF와 MLP part에 각각 다른 embedding을 사용한 후, 마지막 hidden layer인 NeuMF layer에서 concat하는 방식을 취했다. 이때 NeuMF layer는 linearity를 가진 GMF와 non-linearity를 가진 MLP를 결합하기 때문에 그 objective function이 non-convexity를 가질 수밖에 없는데, 이를 해결하기 위해 NeuMF layer를 pre-train 했다고 한다. pre-train 시킬 때는 optimizer로 Adam을 사용하고, 이후 학습시킬 때는 vanilla SGD를 사용해 non-convexity를 최대한 극복하고자 하였으며, 위처럼 모델의 두 파트를 concatenate weights(alpha)로 학습하도록 했다. (momentum에 기도하는 마음은 그럴 듯 하지만 이렇게 했을 때 local minimum에 빠지지 않으리라는 이론적 근거는 존재하지 않는다.)
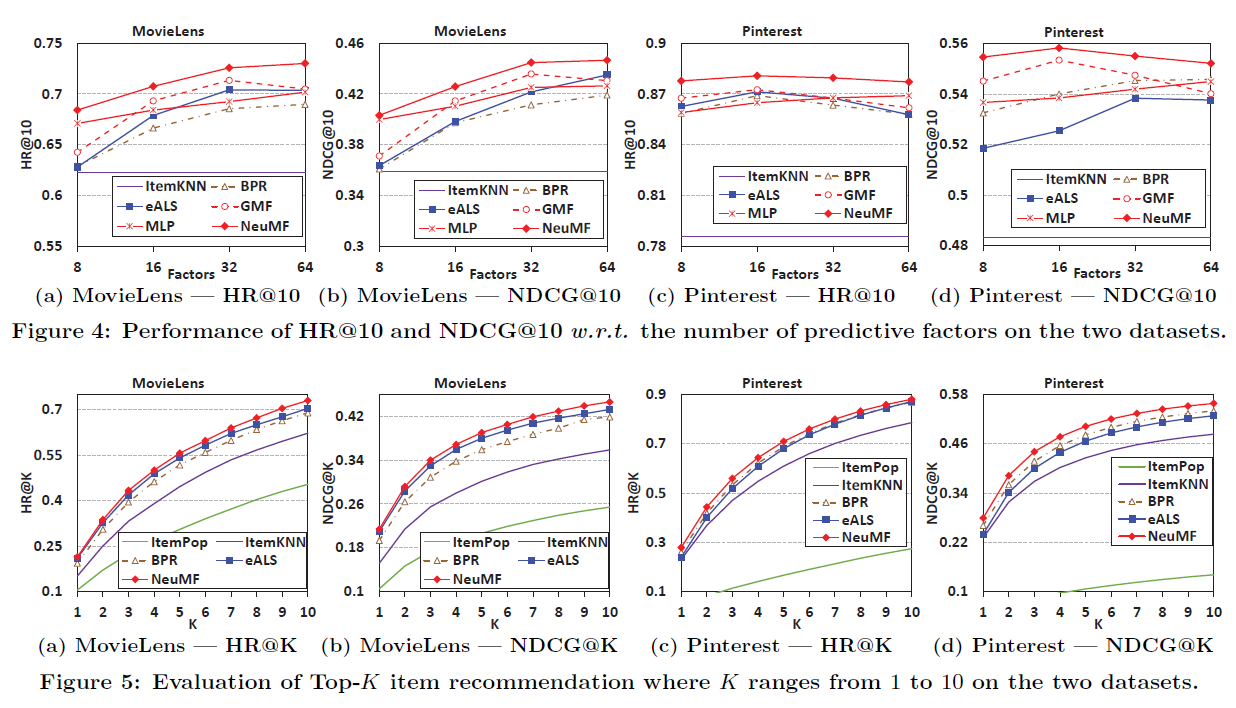
이후에는 성능 자랑 후 마무리.
[느낀점 / 소감]
- 사실 간단한 모델인데, 나는 공부할게 너무 많다.
- pointwise / pairwise / listwise loss에 대해 더 공부해야한다. (BPR 논문 읽자)
- squared loss를 목적 함수로 사용하고자 할 때는 target의 분포가 Gaussian distribution임을 가정하는 등의 주의점?에 대해 공부할 필요가 있다.
- 논문 공부하는게 생각보다 재밌다.
'AI > 추천시스템(RecSys)' 카테고리의 다른 글
| [추천시스템/RecSys] RecBole 라이브러리 (0) | 2022.04.08 |
|---|---|
| [논문 리뷰] BPR: Bayesian Personalized Ranking from Implicit Feedback(2009) (0) | 2022.03.19 |
| [추천 시스템/RecSys] 딥러닝을 활용한 추천 모델 DeepFM, DIN, BST (0) | 2022.03.17 |
| [추천 시스템/RecSys] CAR(Context-aware Recommendation), FM, FFM (0) | 2022.03.15 |
| [추천 시스템/RecSys] KNN과 ANN / ANNOY, HNSW, IVF 등의 방법론 (0) | 2022.03.12 |




